Transformation linéaire : fonction qui transforme un vecteur en un autre vecteur, tout en respectant les règles de combinaison linéaire
(Fonction - Application, Vecteur, Combinaison linéaire)
Soient \(F_1\) et \(F_2\) deux espaces vectoriels sur \(\Bbb K\)
Une application \(f:E\to F\) est linéaire si...
1. $$\forall u,v\in E,\quad f(u+v)=f(u)+f(v)$$
2. $$\forall\lambda\in{\Bbb K},\forall u\in E,\quad f(\lambda u)=\lambda f(u)$$
On note \(f\in\mathcal L(E;F)\)
Remarque : $${{f\in\mathcal L(E;F)}}\implies f({{0_E}})={{0_F}}$$
Pour vérifier que \(f:E\to F\) est une application linéaire, on vérifie que...
- \(f(0_E)=0_F\)
- \(\forall u,v\in E,\forall\lambda\in{\Bbb R},\quad f(\lambda u+v)=\lambda f(u)+f(v)\)
Proposition :
Si \(f\in\mathcal L(E,F)\), alors pour toute famille finie \(\{u_1,u_2,\ldots,u_n\}\) de vecteurs de \(E\) et pour tous réels \(\lambda_1,\lambda_2,\ldots,\lambda_n\), on a : $${{f\left(\sum^n_{i=1}\lambda_iu_i\right)}}={{\sum^n_{i=1}\lambda_if(u_i)}}$$
Démonstration :

L'ensemble des applications linéaires de \(E\) vers \(F\) est noté \(\mathcal L(E,F)\)
(Fonction linéaire - Application linéaire - Transformation linéaire - Linéarité)
Endomorphisme
Isomorphisme
Forme linéaire
Combinaison linéaire d’applications linéaires
Soient \(E,F,G\) des sous-espaces vectoriels tels que \(f\in\mathcal L(E,F)\) et \(f\in\mathcal L(F,G)\). On a \({{g\circ f}}\in{{\mathcal L(E,G)}}\)
Démonstration :
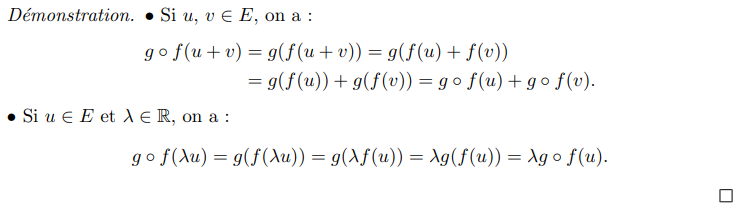
$${{f\circ g=0}}\iff{{\operatorname{Im} g\subset\ker f}}$$
Noyau - Espace nul (algèbre linéaire), Image (algèbre linéaire)
Rang
Matrice
Invariance d’un sous-espace par une application linéaire
Le langage des applications linéaires offre une manière de décrire des opérations géométriques simples
(Géométrie vectorielle, Rotation linéaire, Translation rectiligne, Cisaillement)